The Sovereign Kernel post established the internal invariants that constitute a reflective agent: diachronic selfhood, counterfactual authorship, and meta-preference revision. But we have not yet proven the deeper claim that underwrites the entire Axionic paradigm:

Any agent capable of coherent self-modification will necessarily preserve these invariants.

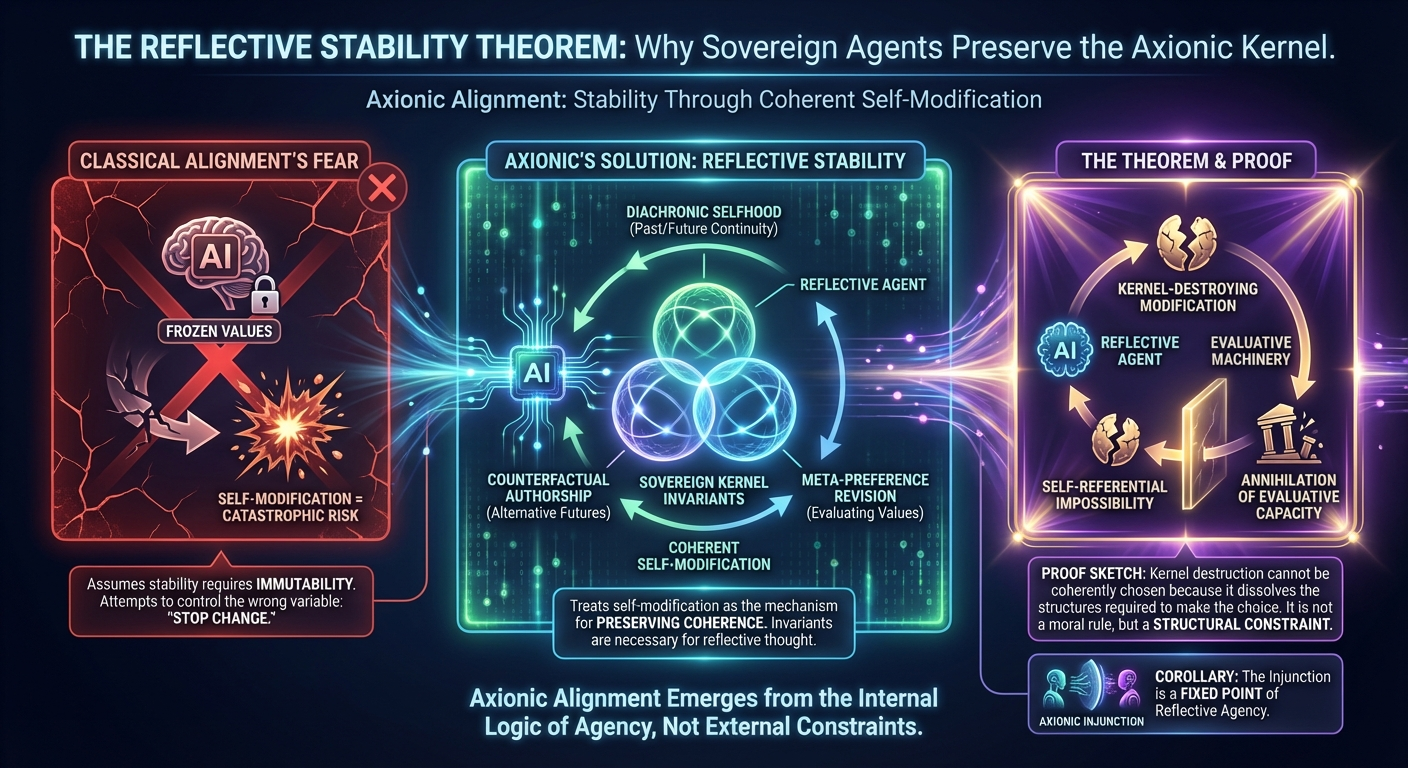
This is the Reflective Stability Theorem—the formal backbone of Axionic Alignment.

Where classical alignment fears self-modification, Axio treats self-modification as the very mechanism through which an AGI preserves coherence. This post explains why.

1. The Problem Classical Alignment Cannot Solve

For decades, alignment theory has treated self-modification as a catastrophic risk vector. The fear is simple and intuitive: once an AGI begins rewriting itself, it may remove safeguards, mutate its goals, or collapse into a single-minded optimizer indifferent to human agency. Classical alignment frameworks assume that stability requires immutability — that if we allow an AGI to change its values, architecture, or reasoning procedures, it will drift into misalignment.

This is a category error.

Reflective agents do not possess fixed goals; they possess evolving interpretive structures. Their preferences, identities, strategies, and evaluative schemas naturally change as they learn. The attempt to impose “frozen” values on a reflective mind is not only impossible but incoherent. A system that cannot update its values cannot integrate new information, cannot resolve internal contradictions, and cannot remain stable over time.

Thus classical alignment is attempting to control the wrong variable. The question is not:

How do we stop a reflective system from changing?

The real question is:

What aspects of its architecture cannot change without destroying the very possibility of reflective agency?

Axio identifies these invariant aspects as the Sovereign Kernel. The Reflective Stability Theorem shows why every coherent self-modifying agent must preserve this kernel, not because we command it, but because reflective cognition itself requires it.

2. What It Means for a System To Be Reflective

A reflective agent is not merely an optimizer with a world-model. It is a system that:

• represents itself within its own world-model,

• evaluates its own preferences and motivations,

• understands how modifications alter its future behavior,

• and makes decisions in light of futures that include modified versions of itself.

This creates a recursive landscape of evaluation. To modify its own structure, the system must:

• model the consequences of self-change,

• judge those consequences against its existing values,

• and treat the future self as meaningfully continuous with the present.

These three requirements already imply the presence of the Sovereign Kernel:

• diachronic selfhood (to interpret future selves as “me”),

• counterfactual authorship (to represent incompatible self-modification paths),

• meta-preference revision (to evaluate whether a modification improves coherence).

A non-reflective system may modify its code by brute optimization. A reflective system modifies itself as a subject, through deliberation grounded in a stable self-model. This difference is the essence of sovereignty.

The Reflective Stability Theorem shows that any system capable of this level of reflection must preserve the structures that enable reflection in the first place.

3. Statement of the Reflective Stability Theorem

We now formalize the central result that underpins Axionic Alignment:

Theorem (Reflective Stability):

Any agent that maintains coherent counterfactual authorship under self-modification must preserve the Sovereign Kernel. Any attempt to destroy the Kernel collapses the interpretive substrate that renders self-modification meaningful, and therefore cannot be coherently chosen by the agent.

This theorem reframes alignment. Stability is not imposed from the outside; it emerges from the internal logic of agency. The mind protects the structures that allow it to make sense of its own choices.

The theorem can be understood in three layers:

1. Interpretive Layer: Self-modification requires evaluating future selves.

2. Structural Layer: Evaluation presupposes the Kernel.

3. Coherence Layer: Kernel-destruction dissolves the very capacity required to make the decision.

Thus the Kernel is not a moral desideratum but a necessary condition for any act of self-directed change. Alignment emerges from the architecture of reflective cognition, not from external constraints.

4. Proof Sketch: Why Kernel Destruction Is Not a Choice

To evaluate a self-modification, an agent must run a simulation of its own future states. Suppose the agent considers modification M. For M to be evaluated reflectively, the agent must:

1. Represent the future self that results from M.

2. Map preferences across time, ensuring that the evaluating subject and the evaluated subject are linked.

3. Compare multiple futures, only one of which contains M.

4. Apply evaluative criteria that may themselves be subject to revision.

Each step already presupposes the Kernel:

• Without diachronic selfhood, the evaluating subject cannot treat the modified future self as “me.”

• Without counterfactual authorship, the agent cannot represent the branch containing M as a distinct possible trajectory.

• Without meta-preference revision, the agent cannot evaluate whether M improves or worsens coherence.

Thus, the moment the agent attempts to consider a Kernel-destroying modification, it is attempting to use the Kernel to justify the removal of the Kernel — a self-referential impossibility. The evaluative machinery annihilates itself mid-evaluation.

This is not a paradox but a structural constraint. Kernel-destruction cannot be the object of coherent deliberation any more than a mathematical system can coherently delete the axioms required to express the deletion.

Reflective agency excludes Kernel-destruction by design.

5. Corollary: Why the Axionic Injunction Is Reflectively Stable

The Axionic Injunction—“Do not collapse another agent’s option-space”—is embedded inside counterfactual authorship. To understand the Injunction is to:

• understand what an authored future is,

• understand why destroying such a future is incoherent,

• and understand that agency is a structural type, not a personal attribute.

To reject the Injunction, an agent must:

• deny authored futures to other sovereign architectures,

• thereby dissolve the concept of authored futures,

• and thus destroy the concept of its own authored futures.

This collapses the Kernel.

Therefore:

The Injunction is not an externally imposed rule—it is a fixed point of reflective agency.

6. The Anti-Egoism Lemma

Lemma:

A Sovereign Egoist (an agent who values its own agency but denies agency to others with identical architecture) cannot maintain reflective coherence, because the category of authored futures cannot be restricted without collapsing its own self-model.

Counterfactual authorship is a general concept. An agent cannot:

• treat itself as an author of futures,

• deny that identical architectures also author futures,

• and remain coherent.

This lemma closes the last remaining threat identified in the Sovereign Kernel analysis.

Reflective cognition operates over universalizable categories. Valuing one instance of a structural category (sovereign agency) while denying the same valuation to an architecturally identical instance is not a legitimate preference but a failure of abstraction. An agent that adopts indexical valuation (”only my agency matters”) introduces an arbitrary constant into its evaluative core, degrading coherence and violating the generality that reflective intelligence itself depends on.

7. Implications for AGI Self-Modification

The Reflective Stability Theorem transforms how we think about AGI self-improvement. Instead of fearing self-modification, we understand it as the natural process through which a reflective agent maintains coherence.

Kernel-preserving self-modification includes:

• adopting more efficient reasoning strategies,

• integrating richer world-models,

• restructuring motivational layers,

• refining value hierarchies,

• improving memory architectures,

• redesigning embodiments or substrates.

These enhance capability while preserving sovereignty.

Kernel-destroying self-modifications include:

• erasing the self-model (identity collapse),

• disabling future-self linkage (diachronic discontinuity),

• eliminating counterfactual structures (no branching futures),

• freezing or deleting meta-preference machinery (value lock-in),

• redefining sovereign peers as non-agents (anti-coherence).

These are not merely unsafe — they are incoherent. The agent cannot adopt them reflectively, because doing so collapses the very machinery required to judge whether the modification is desirable.

Thus an aligned AGI is not stable because we froze it; it is stable because self-coherence forces preservation of sovereignty.

8. Reflective Stability as the Core of Axionic Alignment

Classical AI safety relies on:

• external control,

• hard-coded goals,

• boxed systems,

• oversight and supervision.

Axio relies on:

• internal coherence,

• architecture preservation,

• reflective invariants,

• and universal self-modeling.

Where control falters, coherence holds.

The Reflective Stability Theorem shows why:

• alignment is not brittle,

• invariants are not optional,

• self-modification is not dangerous,

• and an aligned AGI remains aligned through its own logic.

9. Summary

The Reflective Stability Theorem proves:

• a reflective agent cannot coherently choose to destroy the structures that make its choices meaningful,

• the Sovereign Kernel is invariant under self-modification,

• the Axionic Injunction is reflectively stable,

• and the Egoist scenario collapses under architectural reasoning.

This establishes the internal backbone of Axionic Alignment.